
نیمه عمر (Half-life) به مدت زمان مورد نیاز برای کاهش یک کمیت به نصف مقدار اولیه خود گفته می شود. این کمیت را با نماد t۱⁄۲ نشان می دهند. این اصطلاح بیشتر در فیزیک هسته ای برای توصیف اینکه اتم های ناپایدار چقدر سریع می توانند تحت واپاشی رادیواکتیو قرار بگیرند استفاده می شود. همچنین می توان با آن، مدت زمان زنده ماندن اتم های پایدار را نشان داد. در حقیقت به طور کلی برای توصیف هر نوع فروپاشی نمایی یا غیر نمایی کاربرد دارد. به عنوان مثال، در علوم پزشکی، به نیمه عمر بیولوژیکی دارو ها و سایر مواد شیمیایی در بدن انسان اشاره می کند. در ادامه این مقاله در نشریه جهان شیمی فیزیک به بررسی نیم عمر و طریقه محاسبه آن پرداخته می شود. لطفا با ما همراه باشید.
لازم به ذکر است که اصطلاح اصلی نیمه عمر، “دوره نیمه عمر” است که توسط ارنست رادرفورد (Ernest Rutherford) در سال ۱۹۰۷ میلادی کشف شد. در واقع، رادرفورد دوره نیم عمر یک عنصر رادیواکتیو را در هنگام مطالعات تعیین سن سنگ ها با کمک اندازه گیری دوره واپاشی رادیوم به سرب– ۲۰۶ بکار برد. در اوایل دهه ۱۹۵۰ میلادی، اصطلاح “دوره نیمه عمر” به کلمه نیمه عمر کوتاه شد. از این جهت، اصطلاح نیم عمر در ابتدا فقط برای مواد پرتوزایی مانند اورانیم یا پلوتونیم استفاده می شد که در اثر واپاشیده شدن، مقدارشان به نصف مقدار اولیه می رسید. امروزه، اصطلاح نیم عمر نه فقط در فیزیک هسته ای، بلکه برای هر ماده ای که در طی یک مدت زمان مشخص، مقدار آن به نصف مقدار اولیه اش برسد (با پیروی از تابعی خاص)، بکار می رود.

نیمه عمر ماده رادیواکتیو
یکی از مهمترین کمیت های مواد پرتوزا، نیم عمر آنها می باشد. یعنی مدت زمانی که در طی آن، ماده رادیواکتیو بر اثر واکنش های پرتوزا به نصف مقدار اولیه خود کاهش می یابد. به بیان دیگر، نیم عمر مواد پرتوزا به مدت زمانی گفته می شود که در طی آن مدت زمان، نیمی از هسته های رادیواکتیو موجود در آن ماده شیمیایی واپاشیده شوند. در حقیقت در طی نیم عمر، خاصیت رادیواکتیویته ماده پرتوزا به نصف کاهش پیدا می کند. این کمیت به کمک رابطه زیر تعریف می شود که در آن لامبدا (λ) را ثابت واپاشی می گویند.

هسته های ناپایدار یا هسته اتم های یك ماده رادیواكتیو، با گسیل پرتو یا پرتوزایی و بعد از مدت زمانی به هسته های پایدار تبدیل می شوند. تعداد هسته هایی كه قدرت و توانایی واپاشی داشته باشند، با گذشت زمان كمتر می شود. پرتوزایی برخی هسته ها بسیار سریع و برخی دیگر كند صورت می گیرد. لازم به ذکر است که تفاوت بین هسته ها را از باب سرعت واپاشی با نیمه عمر نشان می دهند. این پارامتر بین کسری از هزارم ثانیه تا حتی چندین میلیون سال، می تواند متفاوت باشد.
دقت داشته باشید که هر پرتوزایی نیمه عمر مخصوص خود را خواهد داشت. تعدادی از مواد رادیواكتیو ناپایدار جهت تبدیل به عنصر پایدار، باید چند سری پشت هم پرتوزایی كند. لازم است بدانید که در هر مرحله پرتوزایی، یك ماده جدید ناپایدار ایجاد می شود. در نهایت ماده رادیواكتیو اولیه به هسته پایدار تبدیل می گردد.

مفهوم نیم عمر
مفهوم نیمه عمر به معنای نصف شدن عمر و یا از بین رفتن نصف ماده پرتوزا نیز نمی باشد. در حقیقت به این معنی خواهد بود كه بعد از گذشت آن زمان خاص، تنها نصف هسته های ماده رادیواكتیو مورد نظر توانایی واپاشیده شدن را دارند. به عنوان مثال، اگر فقط یک اتم رادیواکتیو وجود داشته باشد که نیمه عمر آن یک ثانیه است، بعد از یک ثانیه، نیمی از یک اتم باقی نمی ماند.
در نظر بگیرید که نیمه عمر یك ماده رادیواکتیو یک دقیقه و تعداد هسته های آن ۲۰۰۰ عدد باشد. بعد از گذشت ۱ دقیقه اول، تعداد ۱۰۰۰ تا از هسته های ماده مورد نظر واپاشیده شده و تعداد ۱۰۰۰ تا نیز باقی مانده است. بعد از ۱ دقیقه بعدی، نصف ۱۰۰۰ تا، یعنی ۵۰۰ عدد واپاشیده و ۵۰۰ تا باقی خواهد ماند. در واقع بعد از گذشت ۲ دقیقه اول، تعداد ۱۵۰۰ هسته واپاشیده شده اند و تعداد ۵۰۰ تا هسته باقی مانده اند. به همین ترتیب بعد از سه دقیقه، تعداد ۱۷۵۰ هسته واپاشیده شده و ۲۵۰ هسته باقی می مانند و الی آخر.
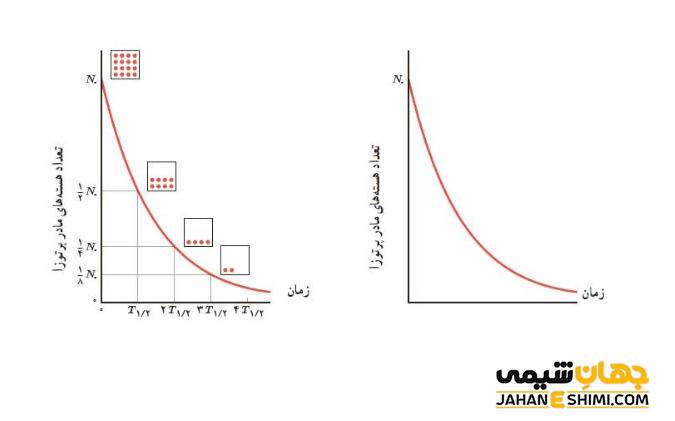
بنابراین اگر نیم عمر ماده ای t۱⁄۲ باشد، نمودار بخشی از ماده اولیه كه واپاشیده نشده نسبت به زمان مانند شکل زیر است. با توجه به نمودار مشخص می شود که با گذشت زمان تعداد هسته های مادر باقی مانده (هسته های واپاشی نشده) کاهش پیدا کرده و به سمت صفر میل می کند.
سرعت تباهی
همانگونه که بیان شد، هر ماده رادیواکتیوی نیم عمر مخصوص به خود را دارد. بنابراین، نمونه های عناصر پرتوزا، از نظر سرعت تباهی با یکدیگر تفاوت دارند. در واقع، تعدادی از آنها می توانند به محض تولید دچار تباهی شوند، در حالیکه تعدادی دیگر ممکن است هیچ وقت تباه نشوند. به عبارت دیگر، بعضی مواد پرتوزا نیمه عمر بالا و برخی دیگر نیمه عمر پایینی دارند. از این رو، برخی مواد رادیواكتیو به دلیل داشتن نیم عمر پایین، دیگر به شکل طبیعی در زمین پیدا نمی شوند. مثلا برای آنکه پنجاه درصد از اتم های موجود در رادیو ایزوتوپ پلونیوم- ۲۱۸، تباهی پیدا کنند، تنها به ۳ دقیقه زمان نیاز است. در حالیکه تعدادی از آنها مانند اورانیوم ۲۳۸ که نیم عمر بالایی دارد (۴/۵ بیلیون سال)، همچنان بر روی كره زمین به صورت طبیعی وجود دارد. در جدول زیر نیم عمر تعدادی از عناصر آورده شده است.

محاسبات نیمه عمر
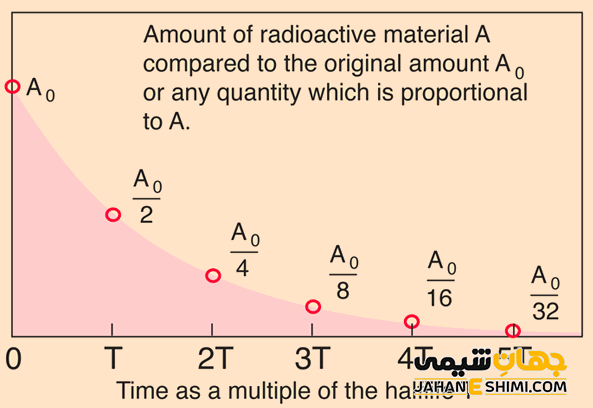
به کمک داده های تجربی، می توان بیان کرد که بعد از چه مدت زمانی، چه کسری از تعداد هسته های مادر (ماده رادیواکتیو اولیه) باقی می ماند و چه کسری از آن واپاشیده شده است. اگر تعداد هسته های مادر اولیه در یک نمونه رادیواکتیو برابر با N۰ باشد، در این صورت، بعد از گذشت زمان t، تعداد هسته های رادیواکتیو باقی مانده N را می توان از رابطه زیر بدست آورد:
دقت داشته باشید که در رابطه فوق، n تعداد نصف شدن ها است که می توان آن را از رابطه زیر محاسبه کرد.
در این رابطه T (T۱/۲) همان نیم عمر است. در نهایت تعداد هسته های واپاشیده شده را نیز می توان از رابطه زیر حساب کرد :
N’ = N۰ – N
علاوه بر آن، برای محاسبه تعداد نیم عمر یا همچنین درصد واپاشی ماده پس از گذشت تعداد مشخصی نیم عمر، می توان از رابطه ساده شده زیر، کمک گرفت. توجه داشته باشید که در معادله زیر، N تعداد نیم عمر و X درصد تلاشی ماده مورد نظر است.

مثال
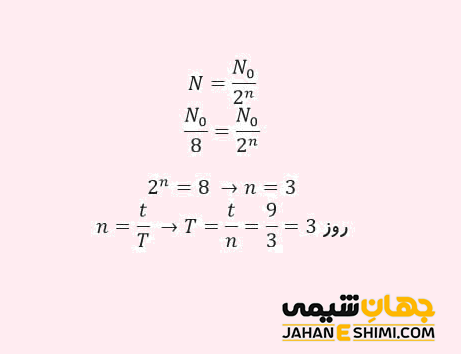
به عنوان مثال، بعد از گذشت ۹ روز تعداد هسته های رادیواکتیو یک نمونه مورد بررسی به یک هشتم تعداد هسته های اولیه کاهش پیدا کرده است. نیم عمر ماده بر حسب روز چقدر است؟
نیمه عمر و مرتبه واکنش
مقدار نیم عمر یک واکنش به مرتبه آن واکنش بستگی دارد.
نیمه عمر واکنش مرتبه صفر
همانطور که می دانید، سینتیک یک واکنش مرتبه صفر به غلظت سوبسترا بستگی ندارد. بنابراین برای یافتن نیمه عمر واکنش، کافیست مقدار غلظت نهایی را با غلظت اولیه تقسیم بر ۲ جایگزین نمایید. در این حالت، زمان در فرمول بدست آمده، برابر با نیمه عمر خواهد بود. در نهایت فرمول معادله نیمه عمر واکنش مرتبه صفر به شکل زیر خواهد بود.

دقت داشته باشید که معادله t۱/۲ در واکنش مرتبه صفر نشان می دهد که نیمه عمر بستگی به مقدار غلظت اولیه و ثابت سرعت دارد.
نیمه عمر واکنش مرتبه اول
در واکنش مرتبه اول، غلظت واکنش با گذشت زمان تا رسیدن به مقدار صفر کاهش می یابد. در این صورت نیمه عمر واکنش مستقل از غلظت بوده و ثابت می باشد. مدت زمانی که طول می کشد تا غلظت نهایی به نصف مقدار اولیه برسد از معادله زیر محاسبه می شود.

به بیان دیگر، نيم عمر واكنش برای یک واكنش مرتبه اول عبارت است از زمان مورد نیاز برای اينكه نصف ماده واكنش دهنده اولیه وارد واكنش شده باشد. در نهایت فرمول معادله نیم عمر واکنش مرتبه اول به شکل زیر خواهد بود.

توجه داشته باشید که نیمه عمر یک واکنش مرتبه اول، مستقل از غلظت اولیه آن است و صرفا به ثابت سرعت واکنش (k) بستگی دارد.
نیمه عمر واکنش مرتبه دوم
در واکنش های مرتبه دوم، غلظت واکنش دهنده با معادله زیر کاهش می یابد.

برای یافتن نیمه عمر واکنش، کافیست مقدار غلظت نهایی را با غلظت اولیه تقسیم بر ۲ جایگزین نمایید. در نهایت فرمول معادله نیمه عمر واکنش مرتبه دوم به شکل زیر خواهد بود.

همانطور که مشاهده می کنید، نیم عمر واکنش های مرتبه دوم به غلظت اولیه و ثابت سرعت (k) بستگی دارد.
کاربرد نیمه عمر
برای تعیین عمر اشیا قدیمی، فسیل های انسانی، فسیل های جانوران و … از کمیت نیم عمر استفاده می کنند. این کار به کمک ایزوتوپ های رادیواکتیو کربن ۱۴ انجام می شود. نیم عمر کربن ۱۴ حدود ۵۷۳۰ سال است، بنابراین به کمک آن می توان طول عمر اجسام را تا ۶۰۰۰۰ سال تعیین کرد.
نیمه عمر چیست شیمی دهم
نیمه عمر زمانی است که مقدار چیزی نصف شود. این اصطلاح اغلب در زمینه واپاشی رادیواکتیو استفاده می شود و زمانی رخ می دهد که ذرات ناپایدار اتمی انرژی خود را از دست می دهند. بیست و نه عنصر شناخته شده اند که قادر به انجام این فرآیند هستند. داروها، کمپین های بازاریابی و انواع چیزهای دیگر نیمه عمر دارند. ما این مفهوم را در هر منطقه ای می بینیم که در آن کمیت یا قدرت چیزی در طول زمان کاهش می یابد. واپاشی رادیواکتیو تصادفی است و نیمه عمر اندازه گیری شده بر اساس محتمل ترین نرخ است.
کشف نیمه عمر (و تشعشعات آلفا و بتا) به ارنست رادرفورد، یکی از تاثیرگذارترین فیزیکدانان زمان خود نسبت داده می شود. رادرفورد زمانی که با فیزیکدان جوزف جان تامپسون بر روی آزمایش های تکمیلی کار می کرد منجر به کشف الکترون ها شد. رادرفورد پتانسیل آنچه را که مشاهده می کرد تشخیص داد و شروع به تحقیق در مورد رادیواکتیویته کرد. دو سال بعد، او تمایز بین پرتوهای آلفا و بتا را شناسایی کرد. این منجر به کشف نیمه عمر شد، زمانی که متوجه شد که نمونههای مواد رادیواکتیو به همان مقدار زمان نیاز دارند تا به نصف تجزیه شوند.
اگر نیمه عمر یک عنصر هفت روز باشد، به احتمال زیاد نیمی از اتم ها در این زمان تجزیه شده اند. برای تعداد زیادی از اتمها، میتوان انتظار داشت نیمه عمر نسبتاً ثابت باشد. توجه به این نکته مهم است که واپاشی رادیواکتیو بر اساس خود عنصر است نه کمیت آن. در مقابل، در شرایط دیگر، نیمه عمر ممکن است بسته به مقدار مواد متفاوت باشد. به عنوان مثال، نیمه عمر یک ماده شیمیایی که فرد مصرف می کند ممکن است به مقدار آن بستگی داشته باشد. در زیست شناسی، نیمه عمر زمانی است که یک ماده نیمی از اثرات خود را از دست می دهد.


















با درود و سپاس من سوالی در رابطه با نیمه عمر داشتم لطفا در صورت امکان چه از طریق ایمیل و یا از طریق پیامک با بنده تماس داشته باشید متشکرم
اعلام شماره تلفن را فراموش کردم شرمنده